Mensuration is the branch of mathematics that studies the measurement of the 2D and 3D figures on parameters like length, volume, shape, surface area, etc. In other words, it is the process of measurement based on algebraic equations and mathematical formulas. Let us learn more about the concept of mensuration, the formulas and solve a few examples to understand it better.
What is Mensuration?
Mensuration can be explained as an act of measurement. We live in a three-dimensional world. The concept of measurement plays an important role in primary as well as secondary school mathematics. Moreover, measurement has a direct connection to our everyday lives. When learning to measure objects we learn to do so for both 3D shapes and 2D shapes. Objects or quantities can be measured using both standard and nonstandard units of measurement. For example, a non-standard unit of measuring length would be handspans. You can even do an activity on it by asking children to measure the length of objects using handspans. Let children notice that while measuring objects using non-standard units there will always be a scope of a discrepancy. Hence the need for standard units of measurement. To measure parameters like length, weight, and capacity we now have units like kilometer, meter, kilogram, gram, liter, milliliter, etc.
3D Shapes Definition
A shape or a solid that has three dimensions is called a 3D shape that has faces, edges, and vertices. They have a surface area that includes the area of all their faces. The space occupied by these shapes gives their volume. Some examples of 3D shapes are cube, cuboid, cone, cylinder and some real-world examples are a book, a birthday hat, and, a coke tin.
2D Shapes Definition
In geometry, 2D shapes can be defined as plane figures that are completely flat and have only two dimensions – length and width. They do not have any thickness and can be measured only by the two dimensions.
Uses of Mensuration
Mensuration is an important topic with high applicability in real-life scenarios. Given below are some of the scenarios.
- Measurement of agricultural fields, floor areas required for purchase/selling transactions.
- Measurement of volumes required for packaging milk, liquids, solid edible food items.
- Measurements of surface areas required for estimation of painting houses, buildings, etc.
- Volumes and heights are useful in knowing water levels and amounts in rivers or lakes.
- Optimum cost packaging sachets for milk etc. like tetra packing.
Important Mensuration Terms
Mensuration deals with the measurement of plane shapes and solid shapes. Let us see some of the important terms used:
| Terms | Definition |
|---|---|
| Area | Area is the amount of space occupied by a two-dimensional figure. It is expressed in square units. |
| Perimeter | Perimeter is the total distance around the shape or the length of the boundary of any closed shape. It is expressed in square units. |
| Volume | Volume is the amount of space occupied by a 3D shape. It is expressed in cubic meter. |
| Surface Area | Surface Area is the total area occupied by the surfaces of a 3D object. They are classified into two - Curved or Lateral Surface Area and Total Surface Area. |
3D Shape Formulas
The following table shows different 3D shapes and their formulas.
| 3D Shape | Formulas |
|---|---|
| Sphere | Diameter = 2 × r; (where 'r' is the radius) Surface Area = 4πr2 Volume = (4/3)πr3 |
| Cylinder | Total Surface Area = 2πr(h+r); (where 'r' is the radius and 'h' is the height of the cylinder) Volume = πr2h |
| Cone | Curved Surface Area = πrl; (where 'l' is the slant height and l = √(h2 + r2)) Total Surface Area = πr(l + r) Volume = (1/3)πr2h |
| Cube | Lateral Surface Area = 4a2; (where 'a' is the side length of the cube) Total Surface Area = 6a2 Volume = a3 |
| Cuboid | Lateral Surface Area = 2h(l + w); (where 'h' is the height, 'l' is the length and 'w' is the width) Total Surface Area = 2 (lw + wh + lh) Volume = (l × w × h) |
| Prism | Surface Area = [(2 × Base Area) + (Perimeter × Height)] Volume = (Base Area × Height) |
| Pyramid | Surface Area = Base Area + (1/2 × Perimeter × Slant Height) Volume = [(1/3) × Base Area × Altitude] |
What is a Sphere?
In geometry, a sphere is a three-dimensional solid figure, which is round in shape

Sphere Formulas
A sphere shape consists of a radius, diameter, circumference, surface area, and volume. Considering a sphere to have a radius of 'r', the following table lists the important formulas of a sphere.
| Name | Formula |
|---|---|
| Diameter | 2 × radius of the sphere |
| Circumference | 2πr, where π is a constant, which takes the value of 22/7 or 3.14 (approx) |
| Surface Area | 4πr2 |
| Volume | (4/3)πr3 |
Cylinder Definition
A cylinder is a 3D solid shape that consists of two identical and parallel bases linked by a curved surface. These bases are like circular disks. The line passing from the center or joining the centers of two circular bases is called the axis of the cylinder shape. The distance between the two bases is called perpendicular distance and is represented as height, “h”. The two circular bases have a distance from the center to the outer boundary which is known as the radius of the cylinder, represented by “r”. The cylinder is a combination of 2 circles + 1 rectangle.
Look at the given image showing the formation of the cylinder shape.

2D Shape Formulas
The following table shows the formulas that are used to calculate the area and perimeter of a few common 2D shapes:
| 2D Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Circle | A = π × r2, where 'r' is the radius of the circle and 'π' is a constant whose value is taken as 22/7 or 3.14 | Circumference (Perimeter) = 2πr |
| Triangle | Area = ½ (Base × height) | Perimeter = Sum of the three sides |
| Square | Area = Side2 | Perimeter = 4 × side |
| Rectangle | Area = Length × Width | Perimeter = 2 (Length + Width) |
What is Circle?
A circle is a two-dimensional figure formed by a set of points that are at a fixed distance (radius) from a fixed point (center) on the plane. The fixed point is called the origin or center of the circle and the fixed distance of the points from the origin is called the radius. Observe the following figure to see the basic parts of a circle, the center, the radius, and the diameter of a circle.

Parts of a Circle
There are many parts of a circle that we should know to understand its properties. A few important parts of a circle are given below.
Circumference: It is also referred to as the perimeter of a circle and can be defined as the length of the boundary of the circle.
Radius of Circle: Radius is the distance from the center of a circle to any point on its boundary. A circle has an infinite number of radii.
Diameter: A diameter is a straight line passing through the center that connects two points on the boundary of the circle. We should note that there can be multiple diameters in the circle, but they should:
- Pass through the center.
- Be straight lines.
- Touch the boundary of the circle at two distinct points which lie opposite to each other.
Chord of a Circle: A chord is any line segment touching the circle at two different points on its boundary. The longest chord in a circle is its diameter which passes through the center and divides it into two equal parts.
Tangent: A tangent is a line that touches the circle at a unique point and lies outside the circle.
Secant: A line that intersects two points on an arc/circumference of a circle is called the secant.
Arc of a Circle: An arc of a circle is referred to as a curve which is a part or portion of its circumference.
Segment in a Circle: The area enclosed by the chord and the corresponding arc in a circle is called a segment. There are two types of segments - minor segment and major segment.
Sector of a Circle: The sector of a circle is defined as the area enclosed by two radii and the corresponding arc in a circle. There are two types of sectors - minor sector, and major sector.
Observe the figure given below which shows all the important parts of a circle.

TRIANGLE
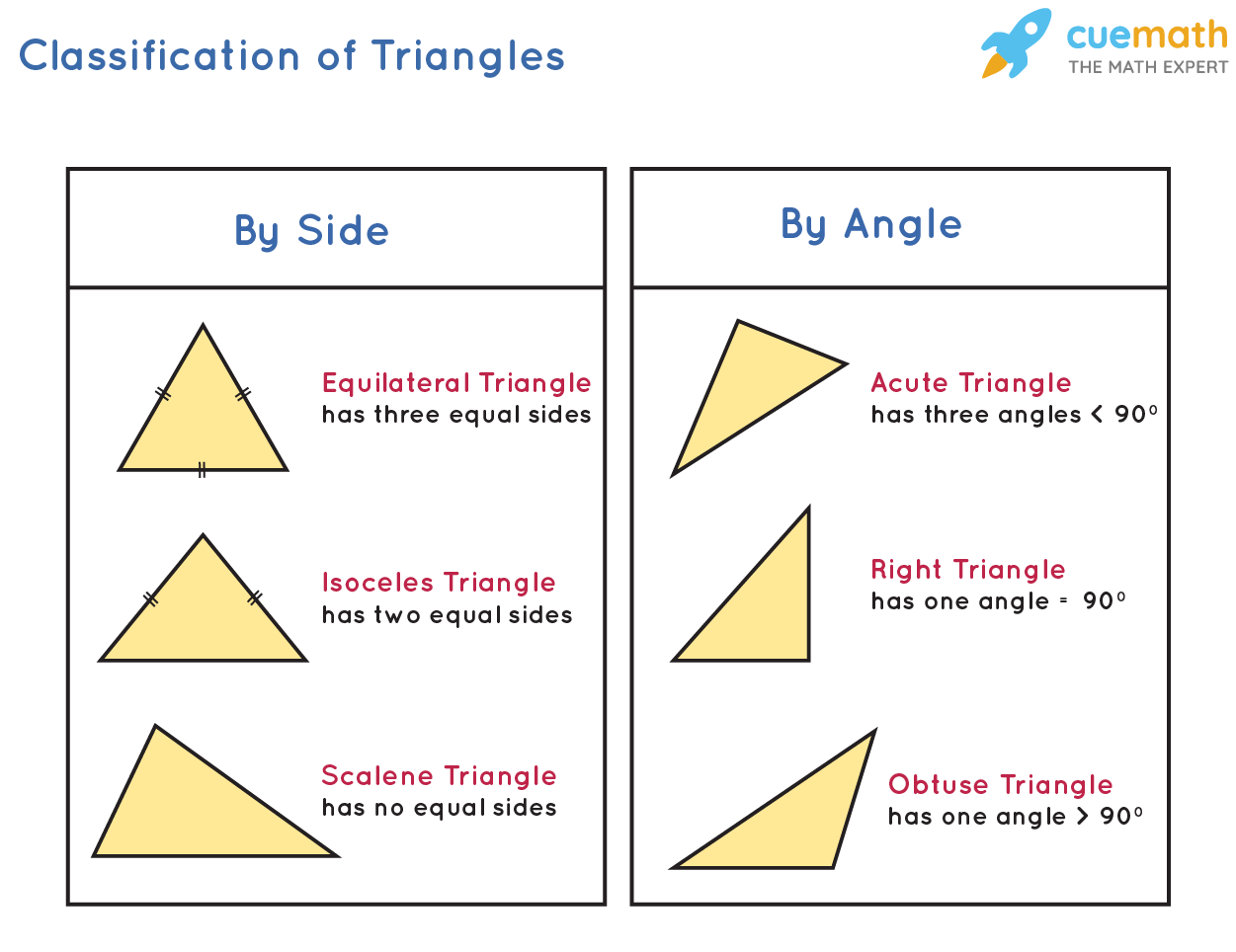
Kinds of Triangles
The following figure shows the different kinds of triangles categorized on the basis of sides and angles.
Perimeter of Triangle
The perimeter of a triangle is the sum of all three sides of the triangle. Observe the triangle given below which shows that the perimeter of the triangle is the sum of all its sides.

Perimeter of Triangle formula = a + b + c
Area of a Triangle
The area of a triangle is the space covered by the triangle. It is half the product of its base and altitude (height). It is always measured in square units, as it is two-dimensional. Observe the triangle ABC given below which shows the base and height of a triangle which are used to calculate the area of a triangle.

Area of ΔABC = 1/2 × BC × AD
Here, BC is the base and AD is the height of the triangle.