Direct Variation

What is direct variation?

• Two variables are said to vary directly if their ratio is constant (k)
  • This is also called direct proportion
  • If If and  (for positive integer n) vary directly then
  •  for some constant k
  • This can be written as 
  • The graphs of these models always start at the origin

How to solve a problem

Identify which two variables vary directly

It might not be x and y

It could be  and 

• Use the given information to find their constant ratio k
  • Also called constant of proportionality
  • Substitute the given values of x and y into your formula
  • Solve to find k
  • Write the equation which models their relationship
  • 
  • You can then use the equation to solve problems

Worked example

A computer program sorts a list of numbers into ascending order. The time it takes, t milliseconds, varies directly with the square of the number of items, n, in the list. The computer program takes 48 milliseconds to order a list with 8 items.

Find an equation connecting t and n.

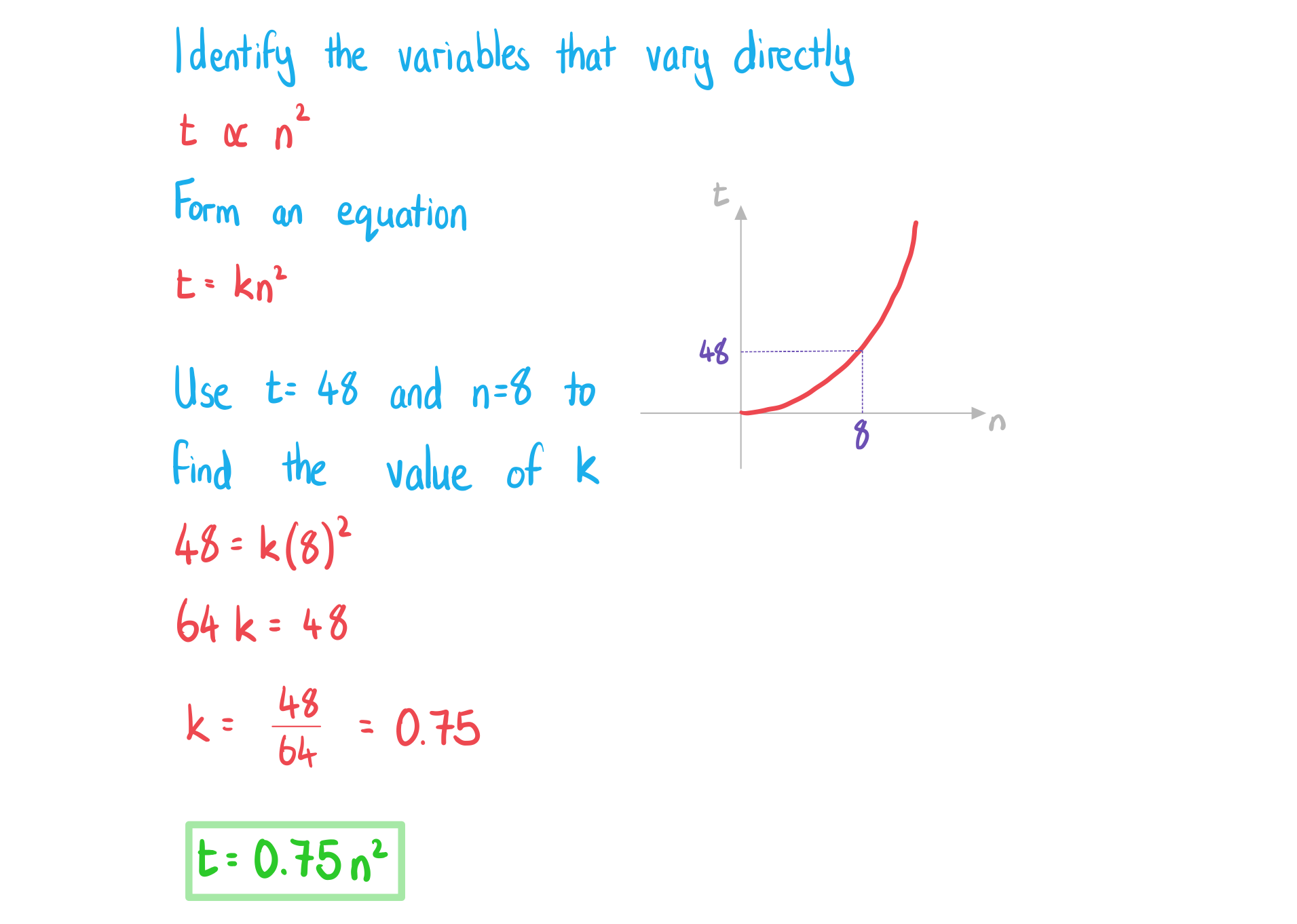
b)

Find the time it takes to order a list of 50 numbers.

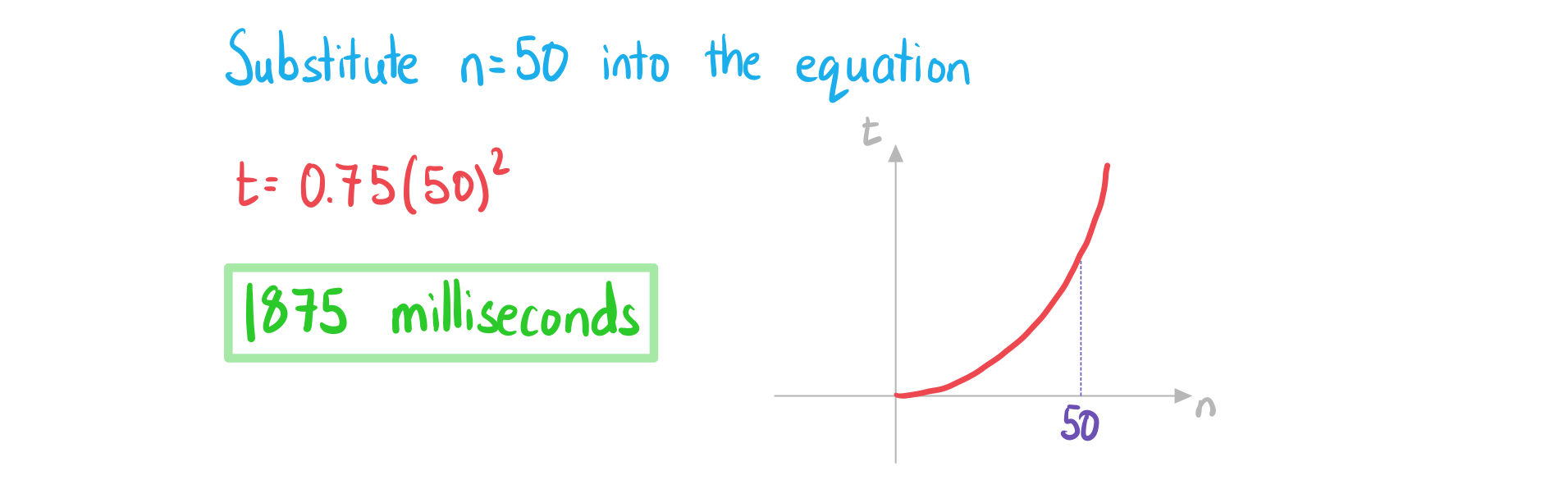
Did this video help you?YesNo

Inverse Variation

What is inverse variation?

• Two variables are said to vary inversely if their product is constant (k)
  • This is also called inverse proportion
• If  and  (for positive integer n) vary inversely then
  • It is denoted 
  •  for some constant k
    • This can be written 
      
• The graphs of these models all have a vertical asymptote at the y-axis
  • This means that as x gets closer to 0 the absolute value of y gets further away from 0
  • x can never equal 0

How do I solve inverse variation problems?

• Identify which two variables vary inversely
  • It might not be x and y
  • It could be  and 
• Use the given information to find their constant product k
  • Also called constant of proportionality
  • Substitute the given values of  and  into your formula
  • Solve to find k
• Write the equation which models their relationship
• You can then use the equation to solve problems

Exam Tip

• Reciprocal graphs generally have two parts/curves
  • Only one – usually the positive – may be relevant to the model
  • Think about why x/t/θ can only take positive values - refer to the context of the question

Worked example

The time,  hours, it takes to complete a project varies inversely to the number of people working on it, . If 4 people work on the project it takes 70 hours to complete.

a)

Write an equation connecting t and n.

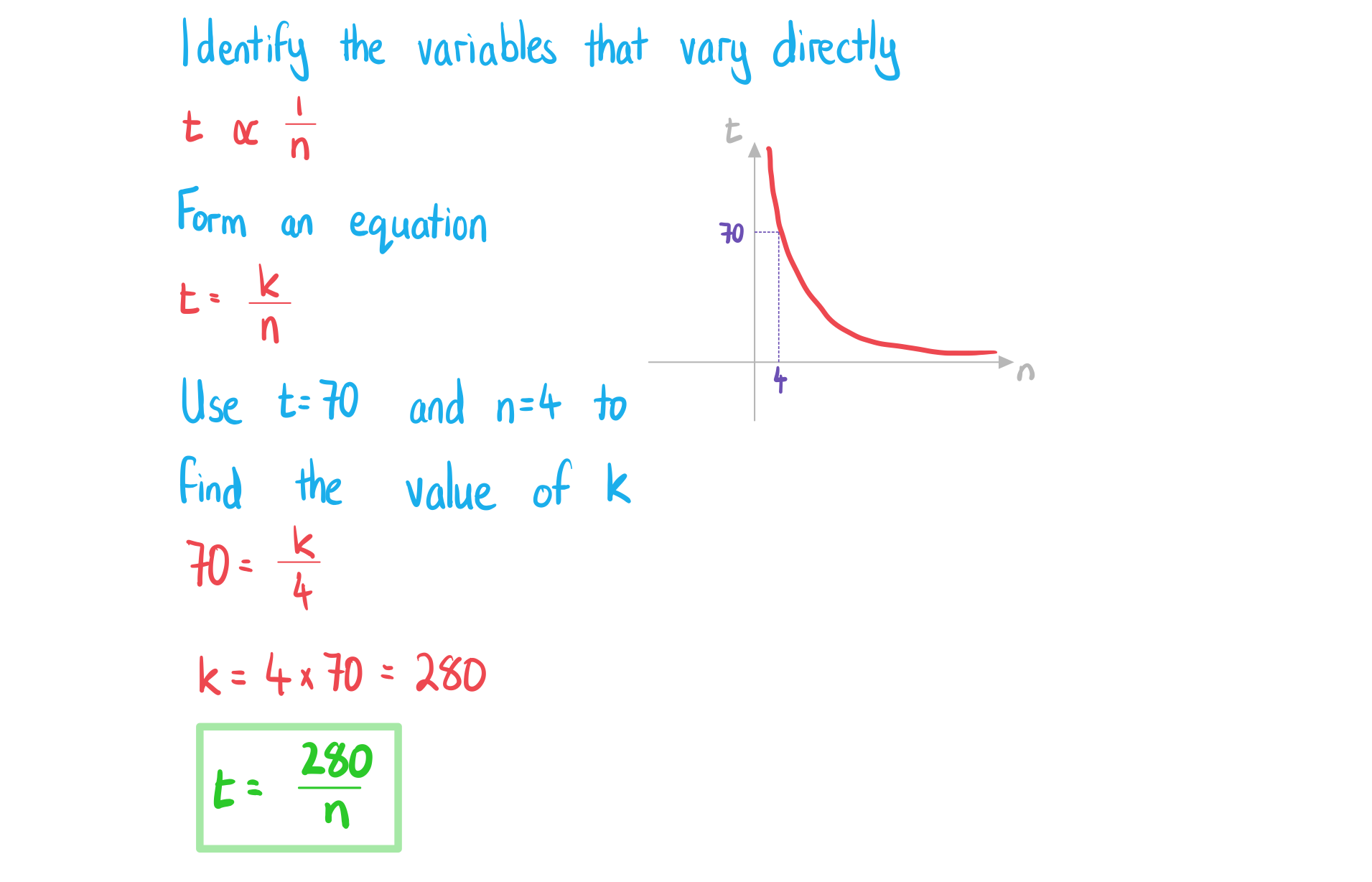
b)

Given that the project needs to be completed within 18 hours, find the minimum number of people needed to work on it.

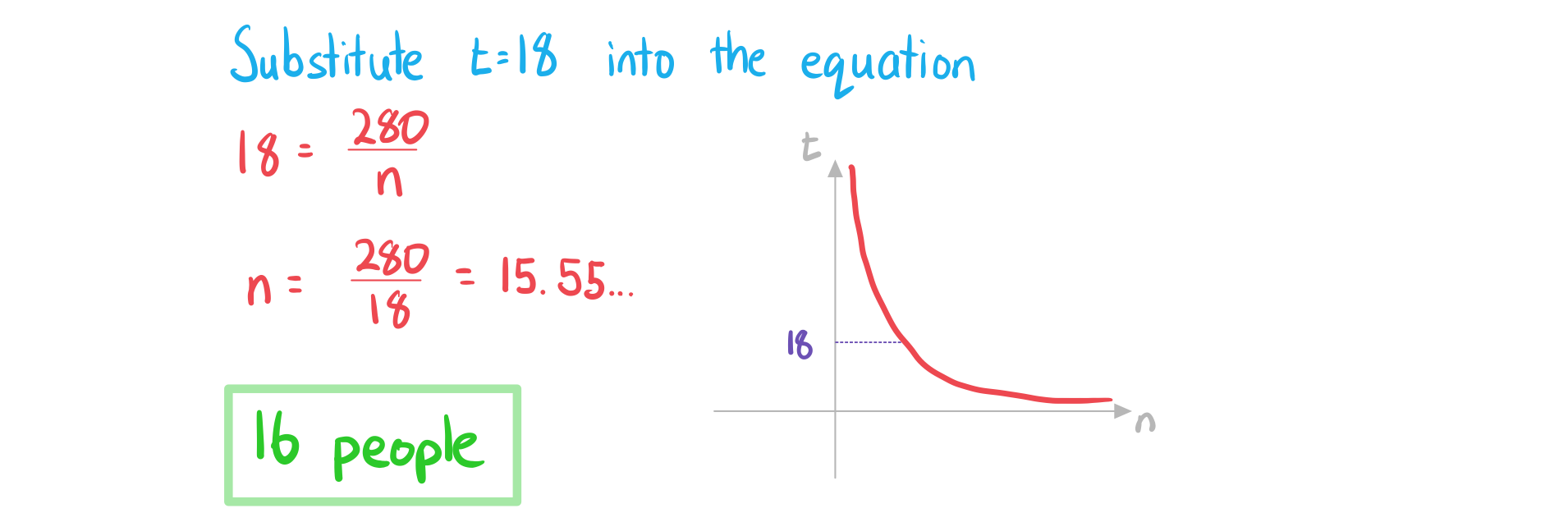
Get unlimited access

to absolutely everything:

• Downloadable PDFs
• Unlimited Revision Notes
• Topic Questions
• Past Papers
• Model Answers
• Videos (Maths and Science)

Join the 100,000+ Students that ❤️ ZimFundi

the (exam) results speak for themselves:

• I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.Beth
  IGSCE Student
• This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!Fathima
  A Level Student
• Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.Kate
  GCSE Student
• Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial topic questions ranked from easy to hard. It's removed a lot of stress from the exams.Sameera
  Parent
• Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 yearsMark
  Chemistry Teacher

Start your 7 day free trial

Test yourselfFlashcardsNext topic

Did this page help you?YesNo

1. Number & Algebra

2. Functions

2.1 Linear Functions & Graphs

2.2 Further Functions & Graphs

2.3 Modelling with Functions

• 2.3.1 Linear & Piecewise Models
• 2.3.2 Quadratic & Cubic Models
• 2.3.3 Exponential Models
• 2.3.4 Direct & Inverse Variation
• 2.3.5 Sinusoidal Models
• 2.3.6 Strategy for Modelling Functions

3. Geometry & Trigonometry

4. Statistics & Probability

5. Calculus

Author: Dan

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.